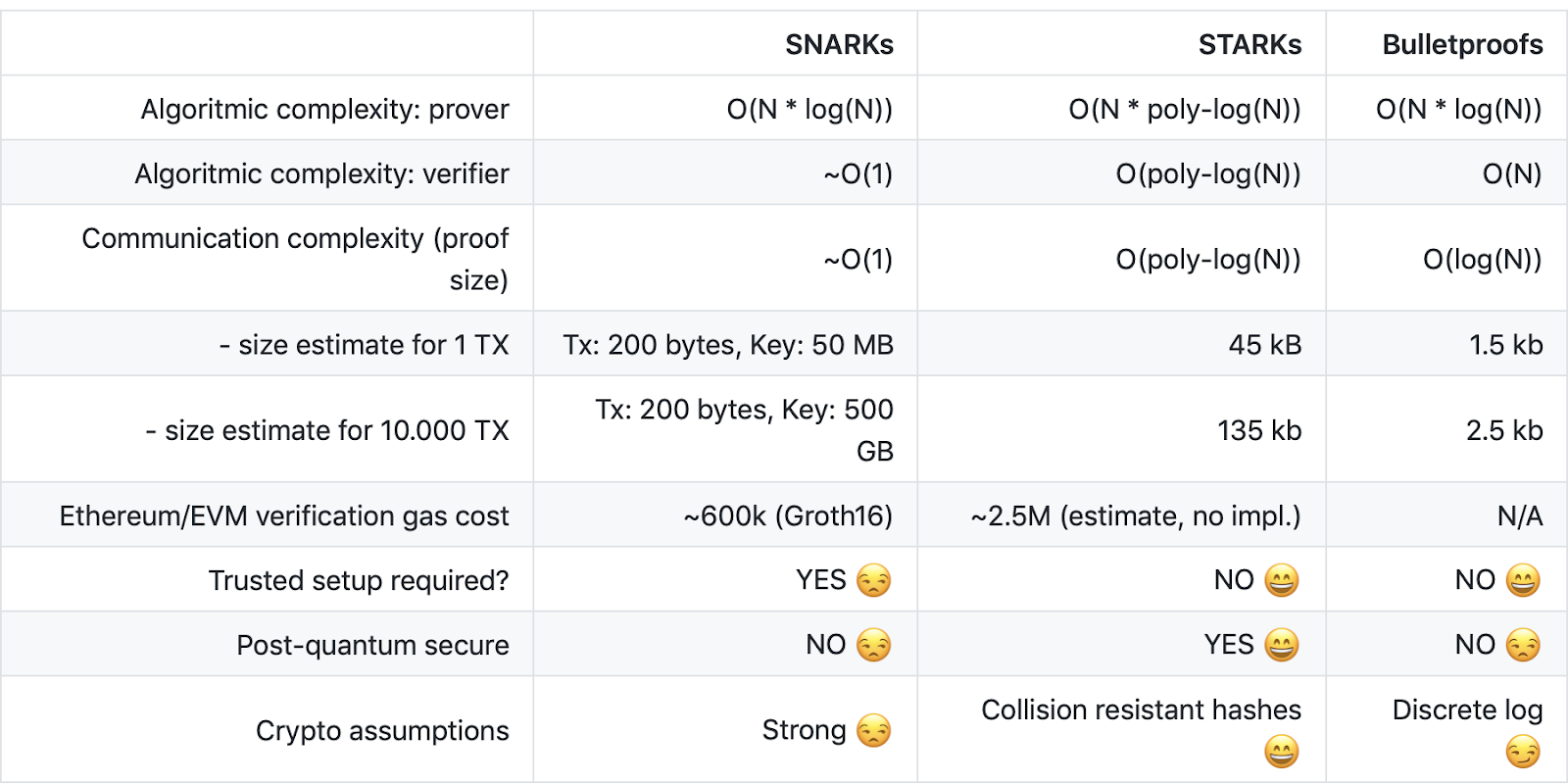
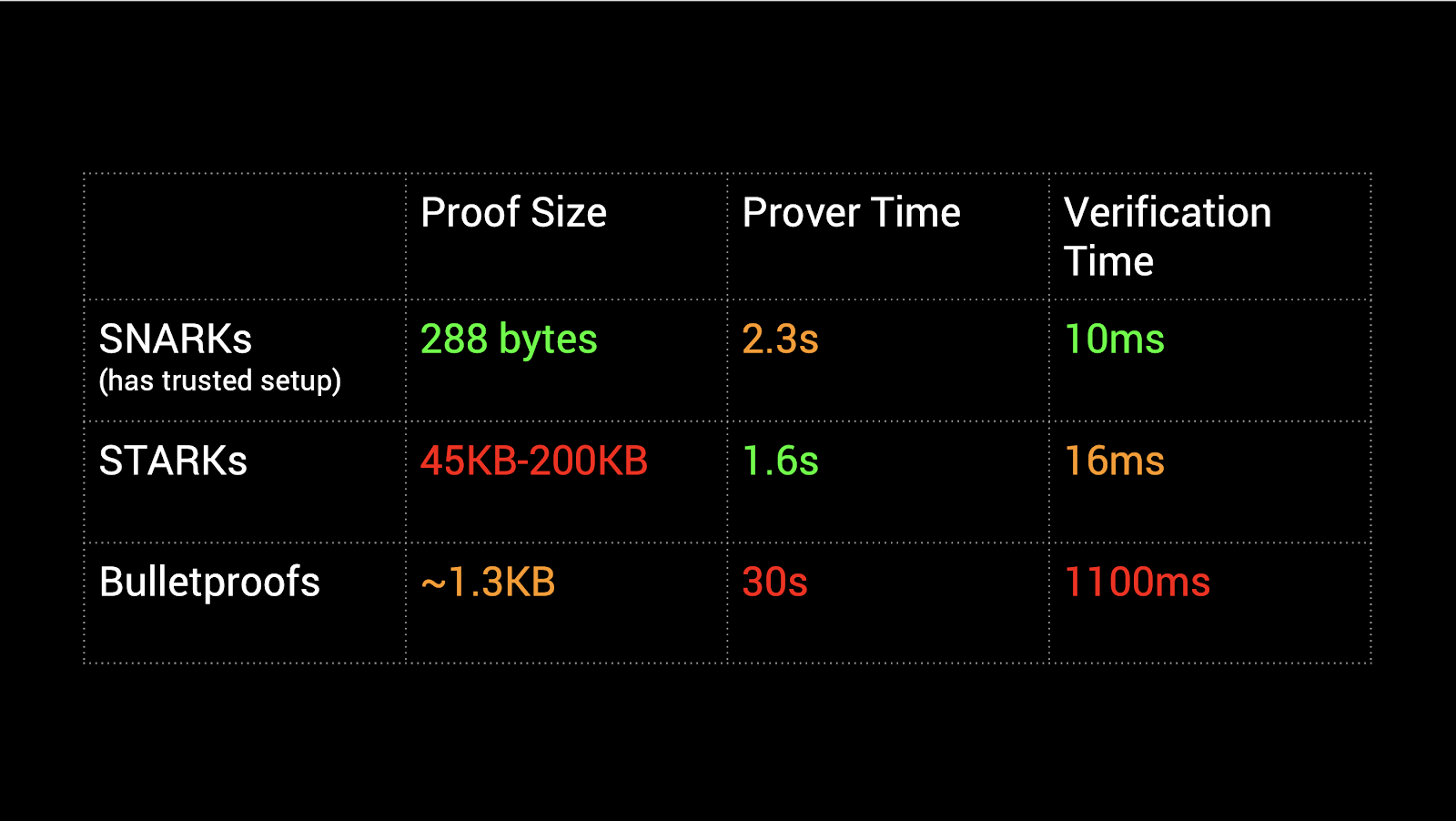
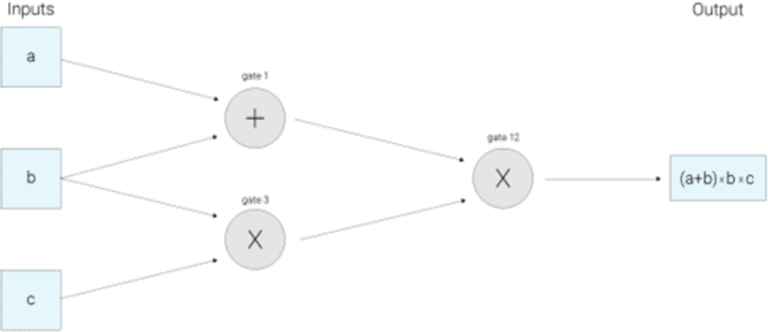
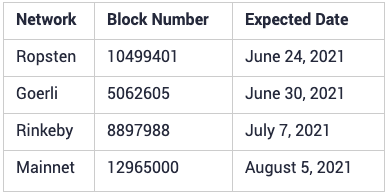
在这篇文章中,我们旨在从实用的角度概述 zk-SNARK。我们会将实际的数学视为一个黑匣子,并尝试围绕如何使用它们建立一些直觉。我们还将给出最近在以太坊中集成 zk-SNARKs 的工作的简单应用。
零知识证明
零知识证明的目标是让验证者能够说服自己,证明者拥有秘密参数的知识,称为见证,满足某种关系,而不会将见证透露给验证者或其他任何人。
我们可以更具体地将其理解为有一个程序,表示为C,接受两个输入:C(x, w)。输入x是公开输入,w是秘密见证输入。该程序的输出是布尔值,即,或者true或false。然后给目标一个特定的公共输入x,证明证明者知道一个秘密输入w,使得C(x,w) == true。
我们将专门讨论非交互式零知识证明。这意味着证明本身是一组数据,无需证明者的任何交互即可对其进行验证。
示例程序
假设 Bob 得到了H某个值的散列,他希望有一个证明 Alice 知道s散列到的值H。通常 Alice 会通过给sBob来证明这一点,之后 Bob 会计算哈希并检查它是否等于H。
但是,假设 Alice 不想向sBob透露该值,而只是想证明她知道该值。她可以为此使用 zk-SNARK。
我们可以使用以下程序来描述 Alice 的场景,这里编写为一个 Javascript 函数:
function C(x, w) { return ( sha256(w) == x );}换句话说:程序接受一个公共散列x和一个秘密值w,true如果w等于SHA-256 散列,则返回x。
使用函数翻译 Alice 的问题,C(x,w)我们看到 Alice 需要创建一个证明,证明她拥有s这样的C(H, s) == true,而不必透露s。这是 zk-SNARKs 解决的一般问题。
zk-SNARK 的定义
甲 ZK-SNARK 包括三个算法 G, P, V 定义如下:
该 密钥生成器 G 需要一个秘密参数 lambda 和程序 C,并产生两个公开可用的按键, 证明键 pk,和一个 验证密钥 vk。这些密钥是公共参数,只需为给定程序生成一次 C。
该 证明 P 作为输入的证明键 pk,公共投入 x 和私人见证 w。该算法生成 证明 prf = P(pk, x, w) 者知道证人 w 并且证人满足程序的证明。
该 验证 V 单位计算 V(vk, x, prf) 其回报率 true ,如果证明是正确的, false 否则。因此,如果证明者知道w 满足 的证人,则此函数返回真 C(x,w) == true。
这里注意lambda 生成器中使用的秘密参数 。该参数有时会使在实际应用中使用 zk-SNARK 变得棘手。这样做的原因是任何知道这个参数的人都可以生成假证明。具体来说,给定任何程序 C 和公共输入, x 一个知道的人 lambda 可以生成一个证明 fake_prf ,以便 V(vk, x, fake_prf) 在true 不知道秘密的情况下 评估为 w。
因此,实际运行生成器需要一个非常安全的过程,以确保没有人知道并将参数保存在任何地方。这就是 Zcash 团队为了生成证明密钥和验证密钥而进行极其复杂的仪式的原因 ,同时确保“有毒废物”参数 lambda 在此过程中被销毁。
我们示例程序的 zk-SNARK
Alice 和 Bob 在实践中如何使用 zk-SNARK 来让 Alice 证明她知道上面例子中的秘密值?
首先,如上所述,我们将使用由以下函数定义的程序:
function C(x, w) {
return ( sha256(w) == x );
}第一步是让 Bob 运行生成器 G 以创建证明密钥 pk 和验证密钥 vk。首先,随机生成 lambda 并将其用作输入:
(pk, vk) = G(C, lambda)小心处理参数 lambda,因为如果 Alice 了解 lambda 的值,她将能够创建假证明。Bob 将与 Alice 共享 pk 和 vk。
Alice 现在将扮演证明者的角色。她需要证明她知道哈希到已知哈希 H 的值 s。 她使用输入 pk、H 和 s 运行证明算法 P 以生成证明 prf:
prf = P(pk, H, s)接下来 Alice 向 Bob 提供证明 prf,Bob 运行验证函数 V(vk, H, prf),在这种情况下会返回 true,因为 Alice 正确地知道秘密 s。Bob 可以确信 Alice 知道这个秘密,但 Alice 不需要向 Bob 透露秘密。
可重复使用的证明和验证密钥
在我们上面的例子中,如果 Bob 想向 Alice 证明他知道一个秘密,则不能使用 zk-SNARK,因为 Alice 无法知道 Bob 没有保存 lambda 参数。鲍勃可能能够伪造证明。
如果一个程序对很多人有用(比如 Zcash 的例子),一个独立于 Alice 和 Bob 的可信独立组可以运行生成器并创建证明密钥 pk 和验证密钥 vk,这样就不会有人了解 lambda。
任何相信该团体没有作弊的人都可以使用这些密钥进行未来的互动。
以太坊中的 zk-SNARK
开发人员已经开始将 zk-SNARKs 集成到以太坊中。这看起来像什么?具体来说,您可以将验证算法的构建块以预编译合约的形式添加到以太坊中。方法如下:在链下运行生成器以生成证明密钥和验证密钥。然后,任何证明者都可以使用证明密钥来创建证明,也是链下的。然后,您可以在智能合约中运行通用验证算法,使用证明、验证密钥和公共输入作为输入参数。然后,您可以使用验证算法的结果来触发其他链上活动。
示例:保密交易
这是一个简单的例子,说明 zk-SNARKs 如何帮助保护以太坊的隐私。假设我们有一个简单的代币合约。通常,代币合约的核心是从地址到余额的映射:
mapping (address => uint256) balances;我们将保留相同的基本核心,除了用余额的散列替换余额:
mapping (address => bytes32) balanceHashes;我们不会隐藏交易的发送者或接收者。但我们会隐藏余额和发送金额。此属性有时称为机密交易。
我们将使用两个 zk-SNARK 将令牌从一个帐户发送到另一个帐户。一份证明由发送方创建,一份由接收方创建。
通常在一个代币合约中,为了使一笔大小值的交易有效,我们需要验证以下内容:
balances[fromAddress] >= value我们的 zk-SNARK 需要证明这是成立的,并且更新后的哈希值与更新后的余额相匹配。
主要思想是发送者将使用他们的起始余额和交易价值作为私人输入。作为公共输入,他们使用起始余额、期末余额和价值的哈希值。同样,接收者将使用起始余额和价值作为秘密输入。作为公共输入,他们使用起始余额、期末余额和价值的哈希值。
下面是我们将用于发送者 zk-SNARK 的程序,其中 x 代表公共输入,w 代表私人输入。
function senderFunction(x, w) {
return (
w.senderBalanceBefore > w.value &&
sha256(w.value) == x.hashValue &&
sha256(w.senderBalanceBefore) == x.hashSenderBalanceBefore &&
sha256(w.senderBalanceBefore - w.value) == x.hashSenderBalanceAfter
)
}接收器使用的程序如下:
function receiverFunction(x, w) {
return (
sha256(w.value) == x.hashValue &&
sha256(w.receiverBalanceBefore) == x.hashReceiverBalanceBefore &&
sha256(w.receiverBalanceBefore + w.value) == x.hashReceiverBalanceAfter
)
}程序检查发送余额是否大于发送的值,并检查所有散列是否匹配。一组受信任的人将为我们的 zk-SNARK 生成证明和验证密钥。我们称它们为 confTxSenderPk、confTxSenderVk、confTxReceiverPk 和 confTxReceiverVk。
在代币合约中使用 zk-SNARKs 看起来像这样:
function transfer(address _to, bytes32 hashValue, bytes32 hashSenderBalanceAfter, bytes32 hashReceiverBalanceAfter, bytes zkProofSender, bytes zkProofReceiver) {
bytes32 hashSenderBalanceBefore = balanceHashes[msg.sender];
bytes32 hashReceiverBalanceBefore = balanceHashes[_to];
bool senderProofIsCorrect = zksnarkverify(confTxSenderVk, [hashSenderBalanceBefore, hashSenderBalanceAfter, hashValue], zkProofSender);
bool receiverProofIsCorrect = zksnarkverify(confTxReceiverVk, [hashReceiverBalanceBefore, hashReceiverBalanceAfter, hashValue], zkProofReceiver);
if(senderProofIsCorrect && receiverProofIsCorrect) {
balanceHashes[msg.sender] = hashSenderBalanceAfter;
balanceHashes[_to] = hashReceiverBalanceAfter;
}
}因此,区块链上唯一的更新是余额的哈希值,而不是余额本身。但是,我们可以知道所有余额都已正确更新,因为我们可以自行检查证明是否已得到验证。
细节
上述保密交易方案主要是为了说明如何在以太坊上使用 zk-SNARKs 的一个实际例子。为了创建一个强大的机密交易方案,我们需要解决一些问题:
- 用户需要在客户端跟踪他们的余额,如果您失去余额,这些代币将无法恢复。余额也许可以使用从签名密钥派生的密钥加密存储在链上。
- 余额需要使用 32 字节的数据并编码熵,以防止反向散列计算余额的能力。
- 需要处理发送到未使用地址的边缘情况。
- 发送方需要与接收方交互才能发送。一个人可能有一个系统,发送者使用他们的证据来发起交易。然后接收方可以在区块链上看到他们有一个“待处理的传入交易”并可以完成它。
原文:https://consensys.net/blog/developers/introduction-to-zk-snarks/