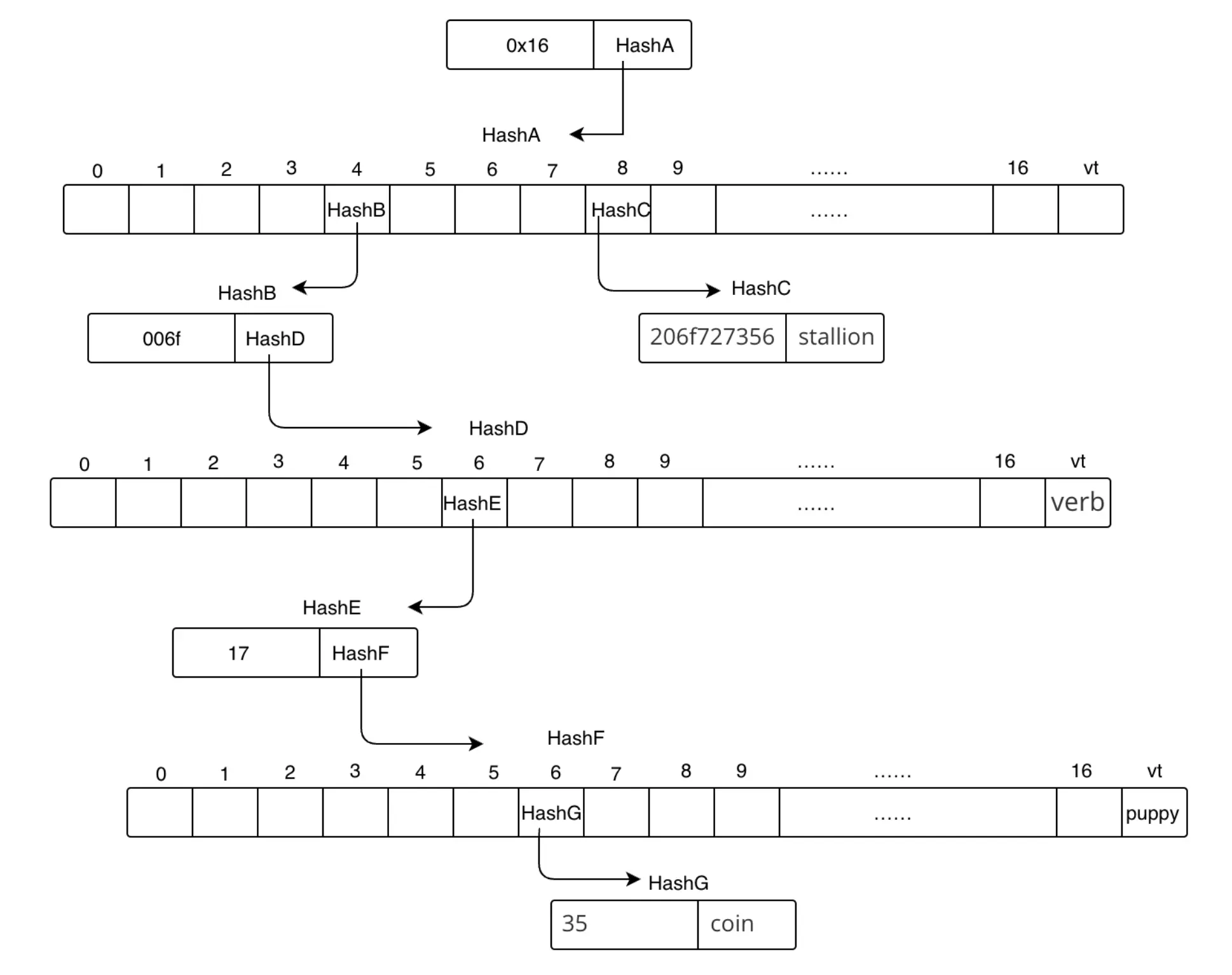
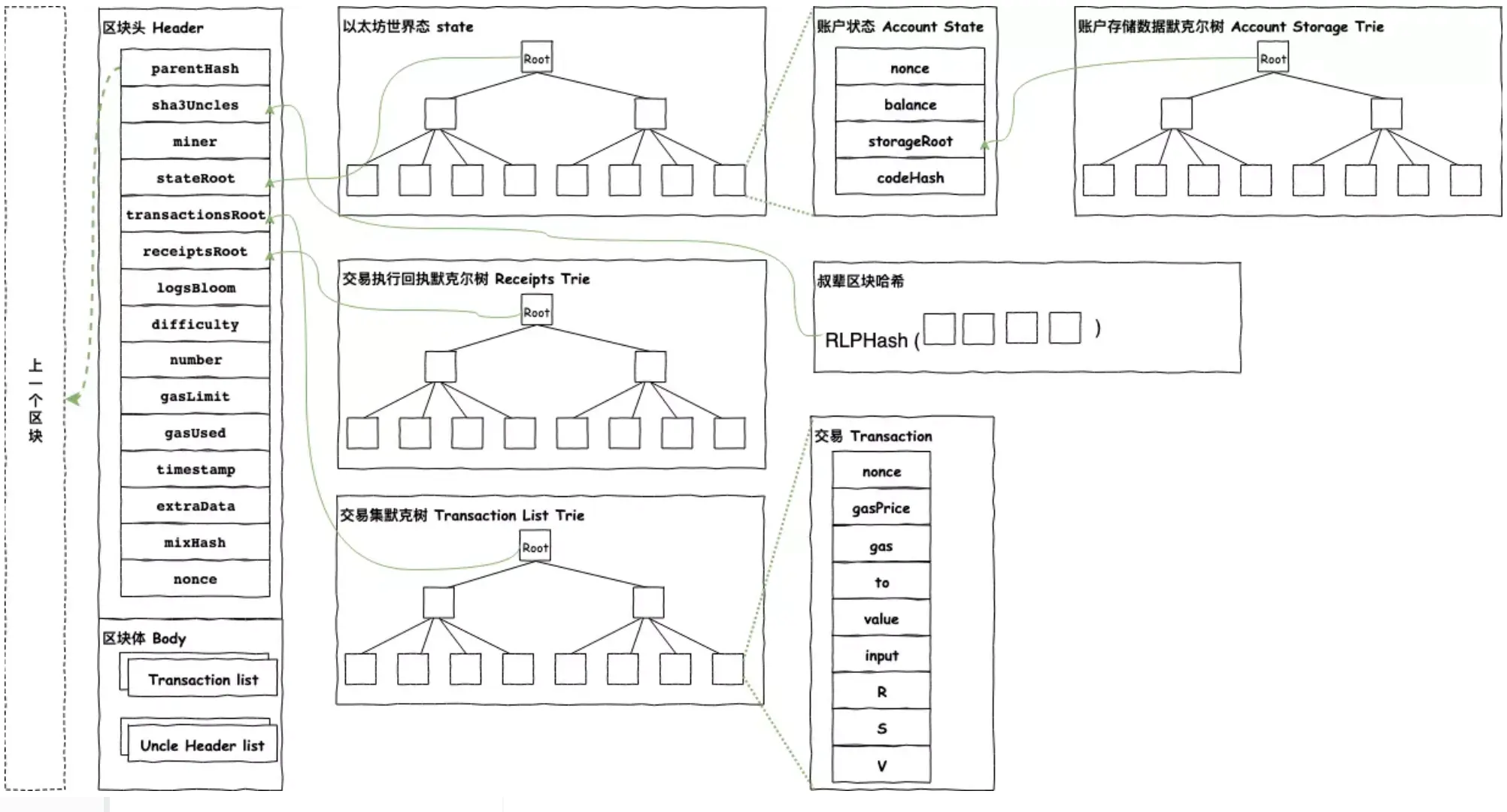
什么是Uniswap？

uniswap是一个进行自动化做市商的项目，该项目的特点是公平，去中心，抗审查，安全。并且uniswap并不会存在特殊群体，参与项目的每个人都是平等的不论你是LP还是Trader。

V1的特点：

• 支持不同的ERC20token进行交换
• 可以加入流动矿池成为LP并获取奖励费用
• 利用公式进行自动定价，每次交易过后都会进行计算定价
• 支持私人定制的交换

每个LP按照一定比例输入ERC20-ERC20的数量之后，会获得一定数量LPtoken，用来表示贡献度，可以根据贡献度来领取池中的奖励（奖励的来源为每次交易收取的费用）。如果想退出的话，可以将LPtoken进行销毁，销毁后会按照LPtoken的比例将两种资金进行返回。

同时可以设置限价单和限时单。

Uniswap如何进行计算

无交易费推导

在整个计算过程中uniswap使用的是x-y-k的模型，即为无论怎样进行交易，保持交易后x * y = k，两种代币的乘积不变。根据这个思想，进行推导

设要用Δx数量的x代币交换Δy代币,则有

(x + Δx) * (y - Δy) = k = x * y
设 α = Δx / x, β = Δy / y，将其代入上式可得
∴ (x + α * x) * (y - β * y) = x * y
∴ (1 + α) * (1 - β) = 1
∴ α = β / (1 - β), β = α / (1 + α)
∴ Δy = α / (1 + α) * y = Δx / (x + Δx) * y
  Δx = β / (1 - β) * x = Δy / (y - Δy) * x

带手续费交易

在实际情况中，每一次交易都会收取一定的手续费用来交易LP，通常手续费为交易量的0.3%，这就表明你输入的Δx并不是全用于计算，实际的计算值为Δx * 0.97%，剩下的作为手续费放入交易池中奖励LP，下面是实际的推导过程：
设要用Δx数量的x代币交换Δy代币,则有

设手续费的比例为ρ, 1 - ρ为γ
(x + Δx * γ) * (y - Δy) = k = x * y
设 α = Δx / x, β = Δy / y，将其代入上式可得
∴ (x + α * x * γ) * (y - β * y) = x * y
∴ (1 + α * γ) * (1 - β) = 1
∴ α = β / ((1 - β) * γ), β = (α * γ) / (1 + α * γ)
∴ Δy = (α * γ / (1 + α * γ)) * y = ((Δx * γ) / (x + Δx * γ)) * y
  Δx = β / (1 - β) * x = Δy / (y - Δy) * (1 / γ) * x
//我们假设ρ = 0.3%，所以γ = 997 / 1000
∴ 上述结果可以表示为：
  Δy = (997 * Δx * y) / (1000 * x + 997 * Δx)
  Δx = (1000 * Δy * x) / ((y - Δy) * 997))

通过上面推导可以看出当ρ为0时就成为了无手续费模式，并且可以发现一个问题，代入手续费之后整个池子的k只会略微变大，这是因为会有部分的费用作为手续费进入池子并不会进入交易当中。也可以理解为，你输入的Δx = 手续费 + 实际的交易的数量

在实际的交易中，会出现以下两种情况：

• 给出交易的x代币数量，计算出y代币的数量
  在这种情况下，输入的x代币会有一部分作为手续费放入池中，其余部分才会被用来做交换。计算时可参考上面手续费交易的结果。
• 给出想要的y代币数量，计算出所需要的x代币数量
  给出想要获取的y代币，计算所需的x代币数量，同时x代币中包含了手续费和实际交换数量。计算时可参考上面手续费交易的结果。

流动性计算

用户不仅可以进行代币的交换，同时还可以成为LP(Liquidity provider)，获取LPtoken用来获取池子中的利息。流动性计算的推导如下

设l = x * y表示两种代币的数量，则有
//提供流动性推导
设α = Δx / x，则有
∴ Δy = Δx / x * y + 1
  Δl = Δx / x * y
∴ x' = x + Δx
  y' = y + Δx * t / x + 1 //这是考虑到solidity语法在计算时的小数会进行向下取整
  l' = l + Δx * l / x

//取消流动性
设β = Δl / l
∴ Δx = Δl * x / l
  Δy = Δl * y / l
∴ x' = x - Δx
  y' = y - Δy
  l' = l - Δl

由于存在向下取整的计算方式，我们将提供和取消两种结合起来看之后会发现，在取消之后剩余的x，y的数量大于提供流动性之前，这是为了保证避免投资者通过这种方式进行获利。如果不使用向下取整的计算方式的话，其实提供和取消之后x，y的数量不会发生变化。同时在提供流动性之后，LP会获取LPtoken，LPtoken数量等于两种代币之积(代币数量更新之后)再开根号。

滑点问题

由于Uniswap是在区块链上的操作，所以可能会导致你看到的价格和实际的价格会有所不同，这是由于交易的确认需要时间，并且交易的顺序不清楚。这样就会导致产生交易滑点，通常为0.5%的滑点保护。而对于滑点的计算我们通常使用(实际成交价格 - 交易时输入的价格) / 交易时输入的价格。当计算出的值满足设定的比例时，即可完成交易。

手续费问题

由于在每笔交易时都会收取一定的手续费，这些手续费会按照LP的持有的token的比例进行分发。这是为了激励用户成为LP并且投入更多的资金，创造更多的流动性。从理论上来说当每一一笔交易发生的时候要将手续费分发给LP，在进行分发的时候可能会使用一个大循环进行分配。但是在实际中这样对用户消耗的gas是很多的，所以这样的方法是不可行的。所以在代码中将手续费的分配放在LP提供流动性和移除流动性的部分，并且维持手续费公平分配的与那里很简单。每次用户进行交易的时候交易的手续费会将每单位的LPtoken的代币的价值提高，而LP在提供流动性的时候会按照当前每单位的LPtoken的代币的价值进行买入LPtoken（变相地理解），举例说明：用户A提供流动性的时候获取了100LPtoken，池子中有1000tokenA，1000tokenB，这时候1LPtoken的价值分别是10tokenA和10tokenB，在经过多次买卖后池子里面有1100tokenA和1500tokenB，这时候1LPtoken对应11tokenA和15tokenB，多出来的这部分即为手续费收益。当用户B想要增加流动性的时候，会按照1LPtoken对应11tokenA和15tokenB的比例进行生成LPtoken，然后按照上面所说的再进行手续费的收益。

质押性挖矿

质押挖矿，在项目中LP可以通过质押自己的LPtoken通过质押一定的时间可以获取质押合约中的奖励代币。再uniswap中LP可以质押自己的LPtoken去获取UNI代币，获取的UNI代币可以去交易所兑换其他的代币，也可以用于参与uniswap的治理，可以通过持有的UNI数量进行投票。

质押挖矿的算法推导

在质押挖矿合约中会进行规定每经过一段时间就会生成一定数量的奖励代币，并且将这些奖励代币按照LP质押的token的数量进行分配给LP。正常思路下我们在分配的时候，会采用循环将质押的用户进行遍历分配。但是在智能合约中使用循环便利的话会消耗大量的gas，这样是不明智的。所以我们要换一种思路来进行奖励的分配。

我们假设质押合约中每秒的奖励为R，合约中质押的代币总数为T，用户A的质押代币数量为a，T包含a
∴ 每秒每一代币的奖励数量为R / T， 用户A每秒获取的代币数量为 a * R / T
我们假设用户A在6秒后取出质押的代币
∴ A所获得的奖励代币数量为：a * R / T * 6

我们再假设B用户在A用户质押4秒后质押了b数量的代币
∴ A所获得的奖励代币数量为：
  a * R / T * 4 + a * R / (T + b) * 2 = a * (R / T + R / T + R / T + R / T + R / (T + b) + R / (T + b))

按照这种思路，我们再进行假设
假设质押的总时长为6秒，A用户在第2秒质押a数量代币，B用户在第4秒质押b数量代币，A用户质押前的代币总数为T'
∴ A所获得的奖励代币数量为：
  a * R / T * 2 + a * R / (T + b) * 2 = a * (R / T + R / T + R / (T + b) + R / (T + b)) = a * (R / T' + R / T' + R / T + R / T + R / (T + b) + R / (T + b)) - a  * (R / T' + R / T')

通过最终的推导式，我们可以得到用户A获得的奖励代币数量等于结算时的累计每份质押代币对应的奖励代币数量之和减去加入时累计每份质押代币对应的奖励代币数量之和再乘以A代币的数量。这样计算的前提是用户A的质押代币的数量不会进行更改，那么问题来了，如果用户对质押代币的数量进行更改了，如何进行计算呢？
其实解决方法很简单，在每次更改数量的时候，对先前数量的质押代币获取的奖励进行结算，然后将变换后的质押代币数量重新进行上述的数量不变的推导。这就是uniswap质押合约代码的逻辑结构，详细的代码可以参考https://github.com/Uniswap/liquidity-staker

问题

1. 质押挖矿的算法推导是不存在问题的，但是在使用时要结合实际情况来进行考虑。由于solidity中对于除法计算使用的是向下取整，所以在上述推导公式中对于每份质押代币对应的奖励代币数量的计算可能会出现结果为0的情况，虽然uniswap的代码中将每秒奖励的数量扩大10**18倍，但是还要考虑扩大之后如果还是小于总的质押代币数量，这个时候可能会出现用户在这段时间的收益为0的情况。这是由于语言特性产生的bug问题。
2. 也要考虑额质押代币数量为0的情况，此时计算收益会出现问题。

转载自：https://learnblockchain.cn/article/5346

一、概念

本文是阅读《深入以太坊智能合约开发》的附录A Merkle Patricia Tree后的知识归纳以及扩展。
默克尔树（Merkle Patricia Tree）在以太坊中是一种通用的，用来存储键值对的数据结构，可以简称为“MPT”，是字典树Redix tree的变种，也是以太坊的核心算法之一。
MPT对于树中节点的插入、查找、删除操作，这种结构可以提供对数级别的复杂度O(log(N))，所以它是一种相对高效的存储结构。

二、如何根据键值对构造默克尔树

2.1 节点类型

树类型的数据结构，都会有节点的概念，MPT也不例外。
MPT中有三种节点类型：branch、leaf、extension：

1. branch（分支）
   1. 由17个元素组成的元组，格式为：(v0,……,v15,vt)。
   2. 其中，v0～v15的元素是以其索引值（0x0~0xf）为路径的子节点数据的keccak256哈希值，如果没有子节点数据则元素为空。
   3. vt为根节点到当前节点的父节点所经过的路径对应的value值，也就是根节点到父节点所经过的路径组成了一个键key，这个key对应的value存在vt里面，如果这个key没有对应的value，那么vt为空。
2. leaf（叶）
   1. 两个元素组成的元组，格式为：（encodePath,value）
   2. encodedPath为当前节点路径的十六进制前缀编码
   3. value是从根节点到当前节点路径组成的键对应的值
3. extension（扩展）
   1. 两个元素组成的元组，格式为：（encodePath,key）
   2. encodedPath为当前节点路径的十六进制前缀编码
   3. key为当前节点子节点数据的keccak256哈希值

总结一下上述的那一堆概念：

• 键值对
• extension节点记录着：路径、子节点的哈希值。
• leaf节点记录着：路径、vlaue。
• branch记录着：以索引值为路径的子节点的哈希值、从根节点到branch的父节点路径组成的键对应的value。
• value值在leaf和branch节点中存放，key被拆解开，最终由extension、leaf的encodePath以及branch的索引值组成。

2.2 十六进制前缀编码

branch和extension元组的第一个元素encodePath就是当前节点路径的十六进制前缀编码（Hex-Pretix Encoding，HP编码）。使用HP编码能够区分节点是扩展结点还是叶子节点。
而HP编码，和当前节点类型还有当前路径半字节长度的奇偶有关。

半字节是4位二进制，即1位16进制。
0xf是半字节，0xff是1字节。
1111是半字节，11111111是1字节。

共有四种前缀：

所以extension节点有两种前缀：0x00、0x1；leaf有两种前缀：0x20、0x3。
可以看到最终前缀在偶数个半字节0x0、0x2后补了一个0，变成了0x00，0x20，目的是为了凑成整字节，避免出现半字节导致长度不便于合并。
HP前缀需要放在原始路径前面去组成HP编码，实例：

2.3 构造一颗默克尔树

上面的概念不容易理解，现在我们以下面的例子，一步步来进行树的构造，帮助我们更好的理解：
我们假设有一组（4个）键值对数据需要用树来存储：

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

为方便解释说明以及阅读，我们把键值对数据的“键”表示为十六进制字符串，“值”则保留为原始字符串。在实际使用时，它们都需要经过特定的编码变换。

1.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

每棵树都有根节点，默克尔树的根节点会保存当前路径和子节点哈希，所以很明显，根节点会是一个extension节点。
上面节点类型介绍了extension格式为：（encodePath,key），encodePath是十六进制的HP编码。分析给出的4个键我们可以得出都是以6开头，后面分为4、8两条路。所以根节点存储的共同路径值为0x6。
由于0x6只有一位，所以路径长度是奇数，节点又是extension类型，所以HP前缀是0x1，组合出来的HP编码：0x16。
所以当前默克尔树如下图：

HashA代表着子节点的哈希值。

2.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

根节点已经找到，但在根节点后出现了两条路，这个时候需要使用branch来处理这种多条路径的情况。

上文说到，branch由17个元素组成的元组，格式为：(v0,……,v15,vt)。其中，v0～v15是以其索引值（0x0~0xf）为路径的子节点数据的keccak256哈希值，如果没有子节点数据则为空。
这里4和8就是索引值，4、8对应元素是其字节点的哈希值。
所以当前默克尔树如下图：

3.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

我们可以观察到，在0x68后只有唯一路径了，即0x6f727356，而value为“stallion”，所以不再分叉的情况下，就不是branch或者extension了，而应该是一个叶节点。

上文提到，leaf节点是两个元素组成的元组，格式为：（encodePath,value），encodedPath为当前节点路径的十六进制前缀编码，value是从根节点到当前节点路径组成的键，所对应的值。

当前节点的路径是0x6f727356，长度是偶数，节点类型是leaf，所以可以得出HP前缀是0x20，HP编码是0x206f727356。所以可得该leaf节点：（0x206f727356,"stallion"）。

所以当前默克尔树如下图：

4.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

说完了8，我们再说说4这部分，路径4后面有共同路径6f，6f后才产生null和6两条分叉。

共同路径6f是一个extension节点，extension节点格式不再介绍，开始计算HP编码，6f长度是偶数，又是extension类型，所以HP前缀为0x00，HP编码为0x006f。

所以当前默克尔树如下图：

5.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

6f后分出了null和6，是多条路径，所以HashD的节点是一个branch节点，6是索引值，索引为6的元素存储着子节点hash；而null是没有的，上文提到：vt为根节点到当前节点的父节点所经过的路径组成的键对应的value。

则代表当前HashD节点该存储从根节点到父节点0x646f组成的键对应的值：'verb'。那么该由HashD的vt保存'verb'。

所以当前默克尔树如下图：

6.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

接下来是共同路径7，一个extension节点，开始计算HP编码，7长度是奇数，又是extension类型，所以HP前缀为0x1，HP编码为0x17。

所以当前默克尔树如下图：

7.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

7后分出了null和6，是多条路径，与第五步相同，HashF是一个branch节点，索引为6的元素存储子节点哈希，vt存储'puppy'的值

所以当前默克尔树如下图：

8.

<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'

好了，现在只剩下一条路径了，表示这最后一个是一个leaf叶子节点，路径为5，路径长度为奇数，索引HP前缀为0x3，HP编码为0x35

所以当前也是最终的默克尔树如下图：

以上就是这棵默克尔树构造的全部过程了，写得很详细，是希望能够为在阅读书籍时没有理顺思路的小伙伴们提供一些帮助。

三、总结

从构造过程中我们可以看出，MPT中节点之间，是通过哈希值来确定的。由于哈希值的特性，只要数据有了微小改动，就会导致根节点改变，所以我们可以用树的根节点来代表整个树中数据的状态，这样就不用保存整个树的数据。

在以太坊中，默克尔树有着大量的应用，比如保存和验证系统中的所有账户状态、所有合约的存储状态、区块中的所有交易和所有收据数据的状态等。

参考

【深度知识】以太坊区块数据结构及以太坊的4棵数

《深入以太坊智能合约开发》

转载自：https://learnblockchain.cn/article/5321