一、介绍

有人把Tendermint当成一个共识，有人把它当成一个通信组件。这都是可以理解的。Tendermint融合了共识和网络通信部分。它类似于一个软件包，通过使用Tendermint可以很容易的开发一个和Cosmos相兼容的区块链（当然，如果使用Cosmos-sdk会更简单，但是会屏蔽更多的细节）。可以把它理解成Cosmos的一个底层架构，提供类似于基础服务的一个平台。Tendermint可以提供一个Cosmos标准的跨链的基础应用。

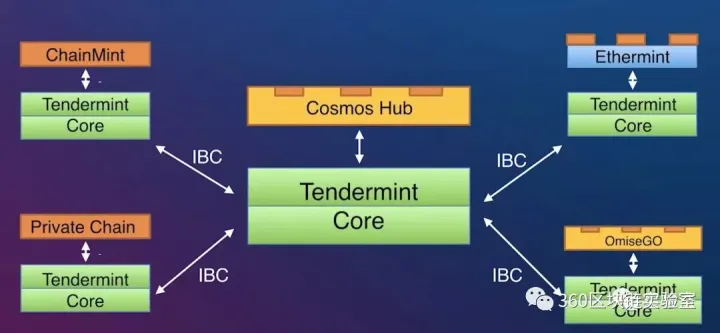
通过上面这个图可以看出Tendermint在整个Cosmos生态中的位置。Tendermint Core是所有Cosmos生态中区块链的核心（上图中的淡绿色部分），提供了DPOS+BFT的共识机制。Cosmos Hub提供了不同区块链的之间的交互和价值转移。各个区块链应用之间通过IBC接口进行通信。

二、整体架构

1、BFT

Tendermint使用的共识算法是拜占庭容错共识协议，它是来源于DLS共识算法。使用这种算法的目的是可以简单方便的解决区块链的分叉机制。这种BFT的机制要求有固定的一组验证人，然后他们会尝试在某个区块上达成共识。每个区块的共识轮流进行，每一轮都有一个提议者来发起区块，之后由验证人来决定是否接受区块或者进入下一轮投票。

Tendermint采用由绝对多数的选票（三分之二）待定的最优拜占庭算法。因此它可以确定的做到：

如果想做恶，必须要有三分之一以上的选票出现问题，并且提交了两个值。
如果任何验证组引起安全问题，就会被发现并对冲突进行投票，同时广播有问题的那些选票。
因为使用了BFT，所以其共识的速度在所有的共识中最相当快速的，很容易达到并维持每秒千笔交易的速度。

2、P2P

Tendermint中的网络底层通信，使用的是一种普通的反应器，它通过参数来查找需要连接的P2P节点，在Tendermint的节点连接中，维护着两组映射来管理连接自己和自己连接的对象，分别称做inbound,outbound.
outbound中，有两种连接，一种是连接时指定的seed,一种是在初始化时检测出来的节点。一般情况下，outbound的数量少于10个。而inbound控制在50个左右的连接。
既然是基于反应器的，那么编程的复杂性就大大降低了。只需要服务监听就可以了。这里不再细节赘述网络通信部分。
网络在启动时，会启动一个协程，定时轮询outbound的数量，来控制连接的稳定性。

3、架构

Tendermint的设计目的是为了创建一个统一的区块链开发的基础组件。通过将区块链中主要的P2P和共识抽象出来，实现区块链开发过程中的组件式管理。这样做的优势有以下几点：

一个是代码重用。对通用的网络通信和共识就不必再重复的造轮子。

二是解放了区块链编程的语言。比如以太坊用go,c++，但是通过Tendermint的抽象后，可以使用任何语言（觉得和当初JAVA才提出时一次编译的想法有些相似啊）。特别是对于智能合约，这个优点就更显得明显了。

4、Tendermint的共识过程

Tendermint共识机制中通过作验证人（Validators）来对区块达成共识，这个在前面已经介绍过，一组验证人负责对每一轮的新区块进行提议和投票。整个共识达成的过程如下图所示。

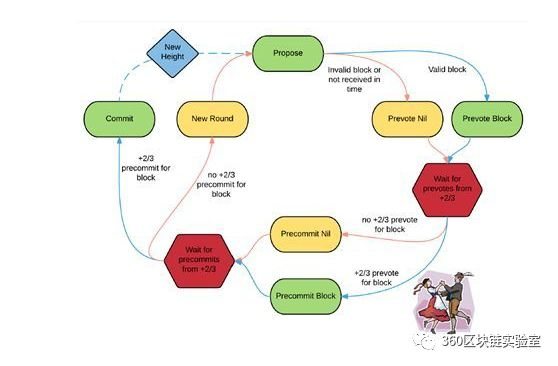
每一轮的开始（New Round），节点对新一轮的区块进行提议。之后，合格的提议区块首先经过一轮预投票（Prevote）。在提议区块获得2/3以上的投票后，进入下一轮的预认可（Precommit），同样是待获得2/3以上的验证人预认可后，被提议区块就正式获得了认可（Commit）。而得到认可的这个区块就被添加的到区块链中。

下面为详细的过程：

在Tendermint算法中，如果遇到对同一特定区块的同意及否决信息同时超过2/3的情况，需要启用外部的维护机制去核查是否存在超过1/3的验证节点伪造签名或者投出双重选票。

5、Tendermint的交易流程

当一个Tx进来时, Tmcore的mempool(MP)会通过mempool connection(一个socket连接，由abci-server提供)调用Application Logic(AL:也就是abci-app，我们自己用任何语言编写的APP逻辑)里的checkTx方法，AL向MP返回验证结果。MP根据验证结果通过或者拒绝该Tx。

Tendermint(TM)把tx暂存在内存池（mempool）里，并把这条Tx通过P2P网络复制给其它TM节点。TM发起了对这条Tx的拜占庭共识投票，所有Tendermint节点都参与了。投票过程分三轮，第一轮预投票（PreVote），超过2/3认可后进入第二轮预提交（PreCommit），超过2/3认可后进入最后一轮正式提交（Commit）

TM提交Tx时依次通过Consensus Connection(一个socket连接，由abci-server提供)向ABCI-APP发送指令BeginBlock-->多次DeliverTx-->EndBlock-->Commit，提交成功后会将StateRoot(application Merkle root hash)返回给TM,TM New出一个区块。

如下图所示的交易流程图：

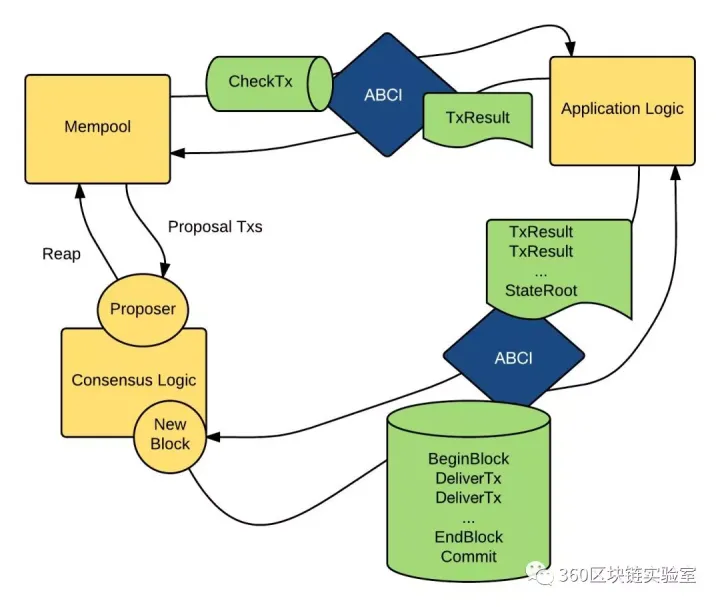
三、总结

通过上面的分析可以看到，其实Tendermint的重点在于共识和P2P，将二者抽象出来的有利之处在于，可以让开发者忽略对网络通信和共识的复杂性。直接进行业务层面的开发，而SDK的封装，进一步减少了业务上对非相关的逻辑的考虑，大大减少了开发者生产一条区块链的复杂度，而这也恰恰是Tendermint和cosmos-sdk所想达到的目的。

转载自：https://zhuanlan.zhihu.com/p/295557240

Why VRF？

场景

在区块链场景中，有的框架会用算法随机产生出块节点与验证节点（如Algorand），甚至解决分叉。按传统的随机算法，按一定的哈希规则随机轮询，选出一个节点来记账/验证。如果这个随机轮询的规则是谁都可以复现的，那么可以推测出将来的某个记账/验证节点，集中攻击它。
为了解决这个问题，就引入了VRF，只有自己能够完成这个哈希过程，而别人只能在他声明之后验证这个过程，防止有人可以提前推测出将来的记账节点。

POS中的权益研磨（Grinding）

（以下来源于以太坊Github上的《Proof of Stake FAQ》）
在任何基于区块链的权益证明算法中，都需要某种机制，来随机从当前活跃验证者集合中选择能够产生下一个区块的验证者。举个例子，如果当前活跃的验证者集合由持有40以太币的Alice，持有30以太币的Bob，持有20以太币的Charlie与持有10以太币的David组成，那么你想让Alice成为下一个区块的创建者的概率为40%，而Bob的概率为30%等（在实践中，不仅要随机选择一个验证者，而是要（随机产生）一个无限验证者序列，只有这样如果Alice不在线的时候，就可以有其他人在过段时间替代她，但是这并没有改变问题的本质）。在非基于区块链的算法中，出于不同的原因也经常需要考虑随机性。
（以下来源Ouroboros白皮书《Ouroboros: A Provably Secure Proof-of-Stake Blockchain Protocol》）
基于PoS的区块链协议最基本的一个问题就是模拟领导者选举过程。为了在股东们之间的选举达到一个真正的随机性，系统中就必须要引入熵(entropy)，但引入熵的机制可能会容易被敌手操作。例如，一个控制一群股东的敌手可能会试图模拟协议的执行，尝试不同的股东参与者的顺序以此来找到对敌对股东有力的继续者。这会导致一个叫做"grinding"的致命弱点，敌对参与者可能会使用计算资源来倾斜领导者选举。

VRF的目的

VRF的目的就是要生成随机值，且无法被预测，同时还要可验证，可重放。

VRF是什么?

VRF是可验证随机函数(verifiable random function)，一方面具有伪随机性，另一方面它还具有可验证性(输出包括一个非交互零知识证明)

• 伪随机性
• 可验证性
  VRF的方式是，实现本地抽签，各个节点自己抽签，如果抽中了之后，大家可以很容易地验证这个结果确实是你生成的。

eg. 假设现在是round 10（第10 轮），节点们可能会轮流抽签，以节点自己的私钥+ 一个全网都知道的随机数（比如是这轮的轮次10）作为输入，生成了一个随机数（0-100）；设置一个条件：100 个节点轮流抽签，谁先抽出来的随机数大于10，就是这一轮的打包者。假设5 号节点抽到了11，可是只有5 号知道其他人不知道，因此他在广播这个随机的同时还需要广播一个零知识证明。通过零知识证明，全网只需要通过5 号的公钥就可以验证，接受5 号为这轮打包者。图解如下：

VRF具体的操作流程？

• 证明者生成一对密钥，PK、SK；
• 证明者计算result = VRF_Hash（SK，info），proof = VRF_Proof（SK，info）；
• 证明者把result，proof，PK递交给验证者；
• 验证者计算result = VRF_P2H（proof)，True/False = VRF_Verify(PK, info, proof)

True表示验证通过，False表示验证未通过。所谓的验证通过，就是指proof是否是通过info生成的，通过proof是否可以计算出result，从而推导出info和result是否对应匹配、证明者给出的材料是否有问题。

抽签有没有必要用VRF？

相比随机预言机

1. 普通哈希Hash(a)=b，所有人都可以重现，检验正确性；
2. VRF是Hash(SIG(sk, a))=b，别人无法复现这个过程。但是可以拿b，pk，和中间信息验证b是跟a对应的。

   相比非对称加密

3. 在密码学签名算法中，大都会引入随机性，也就是对相同信息的多次签名会得到不同的签名值，因此矿工可以不断对相同的输入SK和block，计算签名，以满足结果小于D。那么理论上任何人都会成为出块者，只要计算足够多次的签名。
4. 有些非对称加密方式得到的随机数不是均匀分布的，如RSA
5. 缺乏零知识，不管使用确定性签名还是随机性签名，都存在个安全隐患。就是一旦将自己的出块凭证公布，任何人都可以公开验证，包括攻击者。那么攻击者可以对出块节点进行攻击，使其不能出块。使用VRFs的方式，矿工只需要公布自己的R表明自己的出块权，当出完块的时候再公布P，那么攻击者就无法在出块之前知道谁具有出块权，因此也就无法实施针对性的攻击。

应用

1. Consensus：共识算法中安全性
   VRF Sortition，Smart Contracts，例如本体，Cardano，Dfinity，Algorand等，不同点在于如何产生输入以及输出怎样用。VRF的返回结果可以用来公开或私密地完成节点或节点群体的选择。eg. Dfinity利用mod操作来唯一，公开的确定一个group。Algorand，Ouroboros Praos是私密选择，即计算出哈希值后，如果哈希值小于某个阈值，节点可以私密地知道自己被选中。
   

本体-VBFT共识算法：

1. 根据VRF 从共识网络中选择备选提案节点，各个备选节点将独立提出备选区块；
2. 根据VRF 从共识网络中选择多个验证节点，每个验证节点将从网络中收集备选的区块，进行验证，然后对最高优先级的备选区块进行投票；
3. 根据VRF 从共识网络中选择多个确认节点，对上述验证节点的投票结果进行统计验证，并确定出最终的共识结果。
4. 所有节点都将接收确认节点的共识结果，并在一轮共识确认后开启新的共识。

Algorand中：

1. 先选打包者，选完打包者选委员会，委员会用BA*进行选区块。
2. 输入值由前一个随机数(最初的随机数是协议给定的)和某种代表高度，轮次的变量进行组合，然后用私钥对之进行签名(或者先签名再组合)，最后哈希一下得出最新的随机数。
3. 条件：①签名算法应当具有唯一性；②避免在生成新随机数时将当前块的数据作为随机性来源之一。

Dfinity中：

交保证金提高门槛，并降低参与节点的数量，然后选打包者，选完打包者选公证人，对区块权重进行排序，选出区块。

Cardano的共识机制-Ouroboros Praos：

在根据Random seed选举slot leader时，通过VRF确保slot leader不被事先计算出来被攻击。

1. IOST的高效分布式分配片
   使用了VRF来进行领头节点的选举，通过VRF得到随机数之后，会将结果进行广播，然后其他节点会进行统计，得到随机数值最小的作为分片领头节点。是一种交互式的选举方式。
2. Key Transparency
   密钥管理系统，使消息传递在不相信服务端的情况下做到点对点的安全上的提升。
3. DNSSEC
   DNS服务的安全性。

参考文献

1. Randao可证公平随机数白皮书
2. 《一文看懂可验证随机函数VRF》
3. Ouroboros:一个可证明安全的PoS区块链协议 白皮书
4. Proof of Stake FAQ
5. 黄祺-区块链中VRF的应用及原理解析 视频资源
6. Cardano(ADA)的共识算法Ouroboros
7. 对可验证随机函数VRF的简明解释
8. VRF wiki
9. VRF原文
10. VRF在区块链中的应用

原文链接：https://blog.csdn.net/shangsongwww/article/details/88797403

2018年是公链技术爆发的一年，诞生了诸多从共识方面创新的项目。由于目前人们普遍认为存在区块链“不可能三角”，这些共识往往要在性能、安全、去中心化、激励机制中做出取舍。例如，EOS达成每秒数千次交易速度是以牺牲去中心化为前提的。然而“不可能三角”从来没有像FLP、CAP这些分布式系统定理一样得到严谨的数学证明，因此有些人认为打破“不可能三角”是有可能的。可验证随机函数VRF被认为是一个有前景的方向。本次为大家带来最近热度非常高的Algorand项目的分析。

1、Algorand共识算法简介

Algorand共识算法是图灵奖获得者Silvio Micali在2017年底提出。Michali是MIT的教授，是一位密码学家和计算机理论学家，在伪随机数以及零知识证明领域很有名。
Algorand共识算法的论文的下载地址：https://people.csail.mit.edu/nickolai/papers/gilad-algorand.pdf

Algorand采用了VRF函数，并结合账户的余额比例，随机确定区块生成以及投票人角色。

所谓VRF（Verifiable Random Function）就是可验证随机函数。

随机数对于区块链技术来说很关键。 本质上，分布式账本的核心问题就是随机选择出块人的问题，这个随机性要能被全网确认，并且不能被操控，也不能被预测， 否则恶意节点通过操控这个随机数就可以操控长链，从而实现双花攻击。

PoW的方案是让大家进行算力竞赛，设置一个计算哈希的难题，谁先算出来谁赢，算力高的赢的概率高，算力低的赢的概率低，以这样的方式保证胜出者是随机的。投入的算力能够体现在哈希值上， 这样全网能够验证，并选择包含最多算力的那条链。恶意节点只能通过提升自己的算力来增加攻击成功的概率。

PoS的方案是选举，大家不用浪费电力去进行算力竞赛，而是文明一点，随机选举一个节点来出块，并且被选中的概率和它拥有的份额相关。 如果“随机”这一步没有问题的话，恶意节点只能通过增加自己的份额，增加自己被选中的概率，从而增加双花攻击的成功概率。 这里有一点比PoW的方案要好就是，要实现攻击，先得成为持币大户，如果攻击成功币价大跌，攻击者也会承受最大的损失。

那么接下来的核心问题就是，这个不能被操控不能被预测的随机数从哪来。传统地PoS方案尝试从链上现有的数据入手，比如使用上一个区块的哈希值，上一个区块的时间戳等等来作为随机数的来源，但这些会带来额外的安全风险。 因为区块本身的信息就是节点写进去的，然后又要根据里面的信息来选举后续的出块者，存在循环论证的嫌疑，安全性不会太好。 这也是传统地认为PoS方案不如PoW可靠的部分原因。

Algorand提出的VRF能够由私钥( SK )以及讯息( X )产生一组可验证的伪随机 (pseudorandom) 数Y以及证明 ⍴。任何人都可以透过Verify函数来检验这个随机字串是否真的是该公钥对应私钥持有者，依照规定使用Evaluate函数所产生，而不是自己乱掰的。更详细一点的VRF三个函示描述如下：

•Keygen(r) → (VK, SK). On a random input, the key generation algorithm produces a verification key VK and a secret key SK pair. •Evaluate(SK, X) → (Y, ⍴) . The evaluation algorithm takes as input the secret key SK , a message X and produces a pseudorandom output string Yand a proof ⍴ . •Verify(VK, X, Y, ⍴) → 0/1 . The verification algorithm takes as input the verification key VK , the message X , the output Y, and the proof ⍴ . It outputs 1 if and only if it verifies that Y is the output produced by the evaluation algorithm on inputs SK and X .

为什么我们需要这么一个大家自己产生，却又要可以被验证的随机字串产生器呢？这是因为在Algorand的拜占庭演算法中，虽然也存在着每一轮不同的区块生产者(称为Leader)以及验证委员会(Committee, Verifiers)，但并不是用「公开选举」的方式来选的，而是透过每个使用者自己对奖的方式来看看自己是不是下一轮的Leader。

algorand就是通过随机算法从一群大范围的验证者中选取一部分验证者运行BFT算法(Micali教授实现的BA*算法)，从而达到提高共识的效果。

无论是在何种BFT的共识机制中，都是由Leader以及Committee来完成区块的发布以及共识决议。例如EOS的dPoS BFT是固定21个BP轮流担任Leader以及投票者、Zilliqa透过PoW加入Committee进行PBFT共识算法。这些比较直观的拜占庭共识演算法都有一个共同特征，就是大家都可以看到下一个区块的Leader是谁，以及负责协议共识的Committee是谁。这造成了一个可能的风险，就是这些区块生产者以及Committee成员容易成为DDOS或是贿赂的目标。

Algorand为了解决这种潜在的风险，利用VRF来掩盖Leader Selection的步骤。可以想像成：一般的BFT在每一轮开始时公平公开选出Leader以及Committee，Algorand则是像在每一轮开始时公布中奖号码，每个使用者都可以自己拿自己的票根对奖，中奖的人即可成为下一轮的Leader(或是Committee Verifier)，但在中奖者自己表明身分前，没有人知道谁中奖，也就是没有人能预测下一轮的Leader以及Committee。当然中奖与否并不是口说无凭，中奖者需要出示中奖证明，而这个证明是大家都可以验证的，这正是我们刚刚说到的VRF。

2、Algorand共识算法缺陷

(1)现实环境的随机选择的空间并不大。

VRF是可以提供了公平且不容易收到伪造和攻击的委员会随机选择方式，但是任何随机数的生成必须依赖大的种子集合才可以有作用，在VRF中假设80%节点是诚实的，Committee需要2000个成员才够大，现实情况是不太可能有这么多成员的。

(2)完全没考虑网络延迟情况。

VRF Committee集合选举时依赖数量庞大的主机通讯的，主机之间相互沟通造成的延迟，必然大大拖慢整个系统的处理速度。

(3)没考虑节点的动态加入和退出情况。

Algorand的下一个区块的发布者是从k个区块之前的所有参与者（在k区块之前的某段链上发过交易的节点）里选。于是，恶意节点想影响下个区块的发布者，他得影响k个区块才行，当k很大的时候，这个影响也是微乎其微。于是，Algorand得到了一个无偏向的随机数产生器。不过，这个做法有一个问题——k区块之前的节点，有可能已经不在线了。而对于这一点，虽然Micali做出了解释，但是个人觉得并不符合实际情况。

(4)签名数据庞大，造成存储浪费并影响性能。

Algorand使用VRF来确定提案组与验证组，这个方式充分发挥了VRF的可验证性优势，且后验优势使得Algorand的共识体系更安全。但是，Algorand进入验证阶段，采用的是一种可扩展的拜占庭容错算法，即BA算法，参与节点通过VRF秘密抽签选出。这一设计使Algorand在验证前必须等待凭证（VRF prove）到来，才能知晓参与节点。而且，由于使用了可扩展的拜占庭容错算法，使得Algorand的验证组规模必须比较大(2000～4000人)，这将导致签名数据异常庞大。根据我们的估算，在平均每组3000个验证节点的规模下，每组的签名数据长达126KB，加上其它信息，通知信息约300K，每块的签名数据可达200064*12=1M（共12组，每组3000人，至少2/3达成共识。ed25519签名数据长度是64。），远超一般门限签名几十个字节，严重浪费存储和容量（因每块存储的交易量将被占用，不存储签名又会影响安全），不仅造成存储浪费，而且更影响性能。

(5)无法构建很好的激励机制

在POW中，提案者得到提案权需要预先付出算力成本，若其提案区块有问题（交易双花），则该提案区块在全网其他节点验证必将失败，从而不但没有铸块收益，还付出了算力成本。

Algorand协议并没有设计经济激励机制，Micali教授曾回应”Algorand协议只需要进行平凡的计算，因此不需要激励”。在没有经济激励机制下，高性能带宽和服务器必然不愿意参与（因为它本身要消耗费用），整个网络会遇到网络本身无法解决的困难。

(6)存在潜在的安全问题

网络用户必须连续访问其私钥，以确定其在每一轮中的VRF状态（即验证者、提议者，或者两者都不是）。

一般认为，对于那些将大量资产存储在区块链上的个人，为了防止攻击，他们应该把私钥以冷存储的方式进行保存。而持续的验证（需要经常签名）会需要高频率地动用私钥，从而增加被攻击的风险。这显然将导致网络中很多诚实的个体（出于安全的考虑）会避免参与验证过程，从而造成区块链缺乏活力的问题。

(7)买断问题

在区块链的婴儿期，系统的通证价值通常较低，其市值也是处在相对较低的水平。Token的发行往往要经过私募-->基石-->公募 等逐步分散的过程，因此很长一段时间里币是集中在少数人手里的，因此任何POS共识都面临着EOS类似的中心化的问题。

(8)没有惩罚问题

Algorand所存在的另一个问题是，没有办法识别“离线验证者”并惩罚它们。因此，在没有惩罚措施来防止无效的情况下，没有经济激励就是一个问题，很多人会选择不为共识做贡献，因此离开这个网络。假设网络中只有10%的诚信节点在不断地进行验证，而其余节点是离线的状态，与此同时，恶意的节点选择保持在线，那其就很容易超过在线委员会节点。这使得恶意节点更容易控制共识。

总的来说，Algorand的VRF和加密抽签后验性给出了一个解决“三角悖论”的很好设计思想，但其在验证环节的设计更偏单纯的学术化理想化，导致其对网络流量、有效通讯数据等实际工程落地思考不够，严重影响了公链运行性能、节点网络规模、账本存储容量和去中心化程度。
转载：https://www.8btc.com/article/348383

在这篇文章中，我们旨在从实用的角度概述 zk-SNARK。我们会将实际的数学视为一个黑匣子，并尝试围绕如何使用它们建立一些直觉。我们还将给出最近在以太坊中集成 zk-SNARKs 的工作的简单应用。

零知识证明

零知识证明的目标是让验证者能够说服自己，证明者拥有秘密参数的知识，称为见证，满足某种关系，而不会将见证透露给验证者或其他任何人。

我们可以更具体地将其理解为有一个程序，表示为C，接受两个输入：C(x, w)。输入x是公开输入，w是秘密见证输入。该程序的输出是布尔值，即，或者true或false。然后给目标一个特定的公共输入x，证明证明者知道一个秘密输入w，使得C(x,w) == true。

我们将专门讨论非交互式零知识证明。这意味着证明本身是一组数据，无需证明者的任何交互即可对其进行验证。

示例程序

假设 Bob 得到了H某个值的散列，他希望有一个证明 Alice 知道s散列到的值H。通常 Alice 会通过给sBob来证明这一点，之后 Bob 会计算哈希并检查它是否等于H。

但是，假设 Alice 不想向sBob透露该值，而只是想证明她知道该值。她可以为此使用 zk-SNARK。

我们可以使用以下程序来描述 Alice 的场景，这里编写为一个 Javascript 函数：

function C(x, w) {  return ( sha256(w) == x );}

换句话说：程序接受一个公共散列x和一个秘密值w，true如果w等于SHA-256 散列，则返回x。

使用函数翻译 Alice 的问题，C(x,w)我们看到 Alice 需要创建一个证明，证明她拥有s这样的C(H, s) == true，而不必透露s。这是 zk-SNARKs 解决的一般问题。

zk-SNARK 的定义

甲 ZK-SNARK 包括三个算法 G, P, V 定义如下：

该 密钥生成器 G 需要一个秘密参数 lambda 和程序 C，并产生两个公开可用的按键， 证明键 pk，和一个 验证密钥 vk。这些密钥是公共参数，只需为给定程序生成一次 C。

该 证明 P 作为输入的证明键 pk，公共投入 x 和私人见证 w。该算法生成 证明 prf = P(pk, x, w) 者知道证人 w 并且证人满足程序的证明。

该 验证 V 单位计算 V(vk, x, prf) 其回报率 true ，如果证明是正确的， false 否则。因此，如果证明者知道w 满足 的证人，则此函数返回真 C(x,w) == true。

这里注意lambda 生成器中使用的秘密参数 。该参数有时会使在实际应用中使用 zk-SNARK 变得棘手。这样做的原因是任何知道这个参数的人都可以生成假证明。具体来说，给定任何程序 C 和公共输入， x 一个知道的人 lambda 可以生成一个证明 fake_prf ，以便 V(vk, x, fake_prf) 在true 不知道秘密的情况下 评估为 w。

因此，实际运行生成器需要一个非常安全的过程，以确保没有人知道并将参数保存在任何地方。这就是 Zcash 团队为了生成证明密钥和验证密钥而进行极其复杂的仪式的原因 ，同时确保“有毒废物”参数 lambda 在此过程中被销毁。

我们示例程序的 zk-SNARK

Alice 和 Bob 在实践中如何使用 zk-SNARK 来让 Alice 证明她知道上面例子中的秘密值？

首先，如上所述，我们将使用由以下函数定义的程序：

function C(x, w) {
  return ( sha256(w) == x );
}

第一步是让 Bob 运行生成器 G 以创建证明密钥 pk 和验证密钥 vk。首先，随机生成 lambda 并将其用作输入：

(pk, vk) = G(C, lambda)

小心处理参数 lambda，因为如果 Alice 了解 lambda 的值，她将能够创建假证明。Bob 将与 Alice 共享 pk 和 vk。

Alice 现在将扮演证明者的角色。她需要证明她知道哈希到已知哈希 H 的值 s。 她使用输入 pk、H 和 s 运行证明算法 P 以生成证明 prf：

prf = P(pk, H, s)

接下来 Alice 向 Bob 提供证明 prf，Bob 运行验证函数 V(vk, H, prf)，在这种情况下会返回 true，因为 Alice 正确地知道秘密 s。Bob 可以确信 Alice 知道这个秘密，但 Alice 不需要向 Bob 透露秘密。

可重复使用的证明和验证密钥

在我们上面的例子中，如果 Bob 想向 Alice 证明他知道一个秘密，则不能使用 zk-SNARK，因为 Alice 无法知道 Bob 没有保存 lambda 参数。鲍勃可能能够伪造证明。

如果一个程序对很多人有用（比如 Zcash 的例子），一个独立于 Alice 和 Bob 的可信独立组可以运行生成器并创建证明密钥 pk 和验证密钥 vk，这样就不会有人了解 lambda。

任何相信该团体没有作弊的人都可以使用这些密钥进行未来的互动。

以太坊中的 zk-SNARK

开发人员已经开始将 zk-SNARKs 集成到以太坊中。这看起来像什么？具体来说，您可以将验证算法的构建块以预编译合约的形式添加到以太坊中。方法如下：在链下运行生成器以生成证明密钥和验证密钥。然后，任何证明者都可以使用证明密钥来创建证明，也是链下的。然后，您可以在智能合约中运行通用验证算法，使用证明、验证密钥和公共输入作为输入参数。然后，您可以使用验证算法的结果来触发其他链上活动。

示例：保密交易

这是一个简单的例子，说明 zk-SNARKs 如何帮助保护以太坊的隐私。假设我们有一个简单的代币合约。通常，代币合约的核心是从地址到余额的映射：

mapping (address => uint256) balances;

我们将保留相同的基本核心，除了用余额的散列替换余额：

mapping (address => bytes32) balanceHashes;

我们不会隐藏交易的发送者或接收者。但我们会隐藏余额和发送金额。此属性有时称为机密交易。

我们将使用两个 zk-SNARK 将令牌从一个帐户发送到另一个帐户。一份证明由发送方创建，一份由接收方创建。

通常在一个代币合约中，为了使一笔大小值的交易有效，我们需要验证以下内容：

balances[fromAddress] >= value

我们的 zk-SNARK 需要证明这是成立的，并且更新后的哈希值与更新后的余额相匹配。

主要思想是发送者将使用他们的起始余额和交易价值作为私人输入。作为公共输入，他们使用起始余额、期末余额和价值的哈希值。同样，接收者将使用起始余额和价值作为秘密输入。作为公共输入，他们使用起始余额、期末余额和价值的哈希值。

下面是我们将用于发送者 zk-SNARK 的程序，其中 x 代表公共输入，w 代表私人输入。

function senderFunction(x, w) {
  return (
    w.senderBalanceBefore > w.value &&
    sha256(w.value) == x.hashValue &&
    sha256(w.senderBalanceBefore) == x.hashSenderBalanceBefore &&
    sha256(w.senderBalanceBefore - w.value) == x.hashSenderBalanceAfter
  )
}

接收器使用的程序如下：

function receiverFunction(x, w) {
  return (
    sha256(w.value) == x.hashValue &&
    sha256(w.receiverBalanceBefore) == x.hashReceiverBalanceBefore &&
    sha256(w.receiverBalanceBefore + w.value) == x.hashReceiverBalanceAfter
  )
}

程序检查发送余额是否大于发送的值，并检查所有散列是否匹配。一组受信任的人将为我们的 zk-SNARK 生成证明和验证密钥。我们称它们为 confTxSenderPk、confTxSenderVk、confTxReceiverPk 和 confTxReceiverVk。

在代币合约中使用 zk-SNARKs 看起来像这样：

function transfer(address _to, bytes32 hashValue, bytes32 hashSenderBalanceAfter, bytes32 hashReceiverBalanceAfter, bytes zkProofSender, bytes zkProofReceiver) {
  bytes32 hashSenderBalanceBefore = balanceHashes[msg.sender];
  bytes32 hashReceiverBalanceBefore = balanceHashes[_to];

  bool senderProofIsCorrect = zksnarkverify(confTxSenderVk, [hashSenderBalanceBefore, hashSenderBalanceAfter, hashValue], zkProofSender);

  bool receiverProofIsCorrect = zksnarkverify(confTxReceiverVk, [hashReceiverBalanceBefore, hashReceiverBalanceAfter, hashValue], zkProofReceiver);

  if(senderProofIsCorrect && receiverProofIsCorrect) {
    balanceHashes[msg.sender] = hashSenderBalanceAfter;
    balanceHashes[_to] = hashReceiverBalanceAfter;
  }
}

因此，区块链上唯一的更新是余额的哈希值，而不是余额本身。但是，我们可以知道所有余额都已正确更新，因为我们可以自行检查证明是否已得到验证。

细节

上述保密交易方案主要是为了说明如何在以太坊上使用 zk-SNARKs 的一个实际例子。为了创建一个强大的机密交易方案，我们需要解决一些问题：

1. 用户需要在客户端跟踪他们的余额，如果您失去余额，这些代币将无法恢复。余额也许可以使用从签名密钥派生的密钥加密存储在链上。
2. 余额需要使用 32 字节的数据并编码熵，以防止反向散列计算余额的能力。
3. 需要处理发送到未使用地址的边缘情况。
4. 发送方需要与接收方交互才能发送。一个人可能有一个系统，发送者使用他们的证据来发起交易。然后接收方可以在区块链上看到他们有一个“待处理的传入交易”并可以完成它。

原文：https://consensys.net/blog/developers/introduction-to-zk-snarks/

新技术之间的冲突

纵观历史，总是有类似的技术大约在同一时间进入市场，寻求类似的结果，但以不同的方式解决问题。当这种市场现象发生时，采用者应该尝试客观地评估每一项技术。

由于 STARK 阵营和 SNARK 阵营都对各自的技术充满热情，我们认为对这两种技术进行客观比较会很有趣。

STARKs 与 SNARKs

快速复习一下，零知识证明技术使一方能够向另一方证明他们知道某些事情，而证明者不必自己传达信息来证明他们的知识。它们既是一种隐私增强技术，因为它们减少了用户之间需要提供的信息量，又是一种扩展技术，因为它们可以允许以更快的速度验证证明，因为它们不包含全部信息非私有系统的信息。

当今市场上最引人注目的两种零知识技术是 zk-STARKs 和 zk-SNARKs。两者都是双方证明知识的方法的首字母缩写词：zk-STARK代表零知识可扩展的透明知识论证，zk-SNARK代表零知识简洁非交互式知识论证。本文将深入探讨从文化和技术的角度分析这两种不同的零知识技术之间的核心差异。此外，这两种零知识技术本质上都是非交互式的，这意味着代码可以部署并自主运行。

下面，我们有几个表格描述了两种技术之间的一些高级差异。我们还将深入研究段落格式的差异。

资料来源：物质实验室

SNARK

2012 年 1 月，加州大学伯克利分校一位名叫 Alessandro Chiesa 的教授与人合着了一篇论文，为他们首次构建的零知识证明创造了术语 zk-SNARK。Zk-SNARK 在其基础上依赖于椭圆曲线来保证安全性。密码学中的椭圆曲线在基本假设下运行，即找到相对于公知基点的随机椭圆曲线元素的离散对数是不可行的。

虽然关于椭圆曲线随机数生成器是否存在后门一直存在很大争议，但整个算法通常仍然是安全的。尽管侧信道攻击中有几个流行的漏洞，但可以通过多种技术轻松缓解。量子攻击确实笼罩在基于椭圆曲线的密码学上，但打破其安全模型所需的量子计算尚未广泛应用。

除了基于椭圆曲线之外，zk-SNARK 还需要可信设置。可信设置是指密钥的初始创建事件，用于创建私人交易所需的证明以及这些证明的验证。最初，当这些密钥被创建时，在验证密钥和发送私人交易的密钥之间有一个隐藏的参数链接。如果用于在可信设置事件中创建这些密钥的秘密没有被破坏，则可以利用这些秘密通过虚假验证来伪造交易，从而使持有者能够执行诸如凭空创建新令牌并使用它们等操作用于交易。由于 zk-SNARKs 的隐私特性，将无法验证凭空创建的代币实际上是凭空创造。话虽如此，信任设置仅在最初需要

因此，基于 SNARK 的网络的用户必须依赖于正确执行可信设置的事实，这意味着与可信设置密钥相关的秘密已被销毁，并且不会由监督仪式的个人持有。对可信设置的依赖一直是 SNARK 批评者最关注的领域之一。话虽如此，开发人员只需要最初使用可信设置，而不是持续使用。

SNARK 的另一个重要批评领域是它们不具有量子抗性。一旦量子计算在很大程度上可用，SNARKs 背后的隐私技术将被打破。当然，SNARKs 的支持者正确地指出，当使用量子计算机时，我们将面临更多问题，例如破坏 RSA 和大多数钱包基础设施。

话虽如此，尽管存在与可信设置相关的问题，但实际上 SNARK 的采用速度比 STARK 快得多的原因有很多。SNARKs 比 STARKs 早几年被发现，这使该技术在采用方面取得了重要的领先优势。Zcash 是较早的数字资产项目之一，它在区块链开发社区中普及了 SNARK 的使用。由于 Zcash 和其他 SNARKs 的采用者，SNARKs 拥有最多的开发人员库、已发布的代码、项目和积极致力于该技术的开发人员。除了 Zcash，新兴的 DEX Loopring 也使用了 SNARK。如果开发人员想开始使用零知识技术，他们在使用 SNARK 方面将比 STARK 获得更多支持。

此外，据估计 SNARK仅需要 STARK 所需气体的 24%，这意味着与 SNARK 进行交易对最终用户来说要便宜得多。最后，SNARKs 的证明大小比 STARKs 小得多，这意味着它需要更少的链上存储。

STARKs

虽然 SNARKs 在文档和开发人员支持方面比 STARKs 有一些明显的优势，但 STARKs 确实提供了一些独特的好处。但首先，让我们从技术角度深入了解 STARK 是什么。

Eli Ben-Sasson、Iddo Bentov、Yinon Horeshy 和 Michael Riabzev 在2018 年撰写了第一篇描述 STARK 的论文。与 SNARK 不同，STARK 的基础技术依赖于哈希函数。马上，依靠散列函数提供了一些好处，例如抗量子。此外，开始在网络中使用 STARK 不需要可信设置。

话虽如此，STARKs 的证明尺寸远大于 SNARKs，这意味着验证 STARKs 比 SNARKs 花费更多的时间，并且也导致 STARKs 需要更多的 gas。

此外，由于缺乏开发人员文档和社区，开发人员将很难使用 STARK。虽然有一些项目创建了基于 STARK 的扩展解决方案，例如STARKWARE，但 SNARKs 社区仍然要大得多。

虽然两个开发者社区都支持 SNARKs 和 STARKs，但以太坊基金会特别表达了对利用 Starks 的 STARKware 的声音支持。事实上，以太坊基金会向 STARKware 提供了 1200 万美元的赠款，这清楚地表明了他们对新兴技术的投入。

此外，虽然与 SNARK 相比，STARK 的文档相形见绌，但技术社区最近为那些希望实施尖端技术的人开发了更多资源。

感谢 Anish Mohammad 的洞察力和 专业知识。

原文：https://consensys.net/blog/blockchain-explained/zero-knowledge-proofs-starks-vs-snarks/